こんにちは。田原です。
コンピュータ・プログラムは、数値を使って各種計算、文字列の検索・加工・表示など様々な情報処理を行います。プログラムを単に使うだけの時はその数値や文字内部表現を把握しておく必要はほとんどありませんが、プログラムを開発する時はこれらを知らないとプログラムを書くことさえままならない場合があります。
しかし、見かけと中身がかなり異なるので意外に理解しそこない易い部分です。そこで、今回は数値や文字の内部表現について解説します。
突然ですが、そろばんは一種のデジタルなメモリです。
五珠(5つ玉)のそろばんは串の数と同じ桁数の10進数を記録できます。傾けたり振ったりしない限り、一度記録した数値はそのまま記録され続けますので、一種のメモリです。
電気的に操作できませんので、コンピュータのメモリとしては使えませんが、人は操作できますので人間にとって「外部メモリ」として使えます。電源不要なので不揮発性ですが、傾けたり振ったりしただけで失われるので実使用上は「揮発性メモリ」ですね。
そして、4つの珠の一番上だけを使うことで2進数を記録することができますので、串1本で1ビット(2進数1桁)を記録することができるわけです。
WEB上にそろばんがいくつかありましたので、確認してみましょう。
そろばんの学習「デジそろ」より、デジそろとデジそろアドバンス
中川雅央(滋賀大学)のホームページより、ウェブそろばん(右下の「数の表示」をON)
4つ玉の一番上の珠だけをいくつか動かしてみて下さい。
2進数を記録することができましたね?
実はこれ意外な程、コンピュータのメモリと似ています。
串が5本の1つ珠そろばんが32個並んでいるとします。
この32個の1つ珠そろばんに0~31の「アドレス」を割り当てます。
ちょっと前のPCは「32ビット」が主流でしたが、串5本のコンピュータは「5ビット」です。
アドレスが5ビットしかないので0(00000)~31(11111)番地までの32個の5ビットのメモリ(そろばん)を扱えます。図にしてみました。

(00100番地以降は0クリアされています。)
00000番地はポインタとしましょう。この00000番地には00011(=3)が入っています。ここはポインタなので00011は「アドレス」ですから00011番地を指しています。
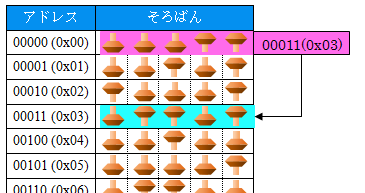
第4回目に出てきた32ビット・ビルド時のメモリの図と見比べてみて下さい。5ビットと32ビットの違いはありますが、それ以外はほぼ同じです。
対応させるとb=00011(=3)、a=01101(=13)となります。

パーソナル・コンピュータの黎明期は、トグル・スイッチとLEDを使ってパチパチと入力していました。ちょうどそろばんの珠を上や下へ弾くのと似ています。

探したら、なんとその動画がYouTubeにありました。世界初の(と称されることもある)パーソナル・コンピュータAltair 8800を操作しています。(1:48くらいからパチパチやってブートローダ・プログラムを入力しています。)
動画では、ブートローダをトグル・スイッチで入力後、実行することでAltair 8800 Basic(かのビル・ゲイツ氏が主要開発者の一人だそうです)を紙テープから読み込んでいます。
そして、Basicの実行開始後は、これが10進数処理を行うため10進数で入出力できるようになります。
ところで、トグル・スイッチやLEDが3つずつ区切られていることにお気づきでしょうか?
2進数を扱う必要がある時、2進数で直接扱うのは分かり難いため、最近は16進数で表現することが多いです。
しかし、16進数で暗算することは当時の人にとっても辛いことでした。しかし、8進数ならちょっと訓練すれば多少の暗算ならできます。10で桁上げの代わりに8で桁上げするだけですので。
そのため、当時は8進数が良く使われていました。8進数1桁は2進数3桁ですから、3つ区切りなのです。
現在もC言語/C++では0で始まる定数は8進数ですが、これは当時の名残りです。
(8進数の10は10進数では8ですから、std::cout << 010 << std::endl;は"8"と表示されます。)
例えば1101 0110 1000 1111のような2進数を示されても、どれくらい大きな数値なのか、パッと理解できない人がほとんどと思います。我々は日常生活では主に10進数を使いますから。ですので、可能ならば10進数に変換したいです。
しかし、困ったことにそろばんと違ってPCには10進数で数値を記録するハードウェアが搭載されていません。また、仮に10進数で記録できたとしても、恐らくそれはトランジスタの電圧で記録されるので人が直接読み取ることもできません。
つまり、人から数値を受け取ったり、人に計算結果を示したりする時に、数値をやり取りするための特別な方法が必要なのです。(前者を入力、後者を出力と表現します。)
古いSF映画などに出てくる紙テープを読み取る学者
紙テープは穴の有り無しで2進数1桁を表現します。これはトランジタのON/OFF状態と違って人が直接目で読み取ることが可能です。モールス信号も長短で1ビットを表現する仕組みですが、それを人は聞き取れますね。それと同じように修練を積めば、紙テープの2進数も読めるようになる筈ですから、昔は本当に紙テープを読める人がいたのだろうと思います。
皆さんもご存知のように多くの場合、キーボードを使います。
キーボードの数字キーを押すことで「数字」がコンピュータへ入力されます。プログラムは数字を必要な桁数受け取り、それが10進数であると解釈して内部表現の数値へ変換します。
このような「数字」はASCIIコードで表現される場合がほとんどです。
ASCIIコードの一部を2進数で表現すると下記となります。(他の文字も決められています。)
| 数字 | ASCIIコード(2進数) |
|---|---|
| 0 | 0011 0000 |
| 1 | 0011 0001 |
| 2 | 0011 0010 |
| 3 | 0011 0011 |
| 4 | 0011 0100 |
| 5 | 0011 0101 |
| 6 | 0011 0110 |
| 7 | 0011 0111 |
| 8 | 0011 1000 |
| 9 | 0011 1001 |
例えば、123[Enter]と入力されたとします。[Enter]は数値の終わりを意味します。(*1)
1が押されるとASCIIコードの0011 0001がプログラムへ伝達されます。
見ても分かるように、このASCIIコードの数字から2進数の0011 0000(=数字’0’のASCIIコードです。)を引くと都合よく、0000(10進数でも0)~1001(10進数なら9)を得ることができます。
この性質を利用して、文字列123を数値へ変換してみましょう。なお、この時「数値」はコンピュータ内部では2進数で表現されていることが多いですが、我々はそれが2進数であることを気にしないといけないケースはかなりレアです。下記のように通常は何進数で記録されているのか気にかける必要はありません。数値は(文字ではなく)数値として捉えておけば十分です。
#include <iostream>
#include <string>
int main()
{
// べた書き
int num=0;
num = ('1'-'0');
num = num*10+('2'-'0');
num = num*10+('3'-'0');
std::cout << num << std::endl;
// 桁数可変
std::string input("123");
num=0;
for (unsigned i=0; i < input.size(); ++i)
{
num = num*10+(input[i]-'0');
}
std::cout << num << std::endl;
return 0;
}
このような処理により入力された複数の「数字」を内部の数値へ変換できます。変換した数値は、ほとんどの処理系で2進数で記録されます。(多くのコンピュータはこの2進数をトランジスタをON/OFFで表現して内部的に保持しています。)
std::cin(std::istream)はこのような変換機能を内蔵していますので、入力された文字列を(自動的に)数値へ変換し数値型の変数へ代入できます。
int num; std::cin >> num;
なお、std::cinが持つ変換機能は、負の数にも対応してますし更に複雑な変換にも対応しています。
(*1)数値の終わり
何か終わりを示す手段を用意していないと、コンピュータはどこまでを数値として解釈すれば良いか分かりませんので、数値の終わりを示す何かが必要です。数値表現に使う以外の文字([Enter]キーもその1つです)が来たら終わりと解釈することが多いです。
コンピュータ内部ではトランジスタのON/OFFの2進数で表現されている数値を、人が理解できるよう10進数で表示したいです。
変換アルゴリズムは下位の桁から10で割り算していけれは良いです。10割った余りに’0’を足すとその桁のASCIIコードになります。
文字列を数値へ変換する時の逆処理なので、3桁の正の数であることが解っている場合にベタ書きすると下記となります。可変長処理は順序の入れ替えを可変長で行うため、少しややこしいです。
#include <iostream>
#include <string>
int main()
{
// べた書き
int num=123;
char c2=(num % 10)+'0';
num = num/10;
char c1=(num % 10)+'0';
num = num/10;
char c0=(num % 10)+'0';
num = num/10;
std::cout << c0 << c1 << c2 << std::endl;
// 可変長対応
num=123;
std::string temp; // tempには最下位桁が先頭に入る
while(num)
{
temp.push_back( (num % 10)+'0');
num = num/10;
}
std::string output; // tempの順序を逆順に入れ替える
unsigned len=temp.size();
for (unsigned i=0; i < len; ++i)
{
output.push_back(temp.back());
temp.pop_back();
}
std::cout << output << std::endl;
return 0;
}
このような処理により、数値を文字へ変換することができます。
そして、std::cout(std::ostream)は、このような変換機能を内蔵していまので、こんなに面倒な処理は不要です。
int num=123; std::cout << num << std::endl;
なお、std::coutが持つ「数値→文字列変換処理」は、当然ですが負の数にも対応してますし、更に複雑な変換にも対応しています。
#include <iostream>
#include <iomanip>
#include <bitset>
void output(int x)
{
std::cout << "16進数 : " << std::hex << x << std::endl;
std::cout << "10進数 : " << std::dec << x << std::endl;
std::cout << " 8進数 : " << std::oct << x << std::endl;
std::cout << " 2進数 : " << std::bitset<8>(x) << std::endl;
}
int main()
{
// 数値→文字列変換
int num=123;
char c2=(num % 10)+'0';
num = num/10;
char c1=(num % 10)+'0';
num = num/10;
char c0=(num % 10)+'0';
num = num/10;
std::cout << c0 << c1 << c2 << std::endl;
// 数値をn進数へ変換して表示する
std::cout << "--- 123 ---\n";
output(123);
std::cout << "--- c0('1') ---\n";
output(c0);
std::cout << "--- c1('2') ---\n";
output(c1);
std::cout << "--- c2('3') ---\n";
output(c2);
return 0;
}
このように数値を文字列へ変換してから、表示されることが重要なことなのですが、更に補足があります。文字列をどのようにして、人が見て文字であると理解できるように表示しているのか?です。
半角文字はASCIIコードで表現されていますが、そのコードから’1’と言う文字を「指定された形状」で表示する仕組みがあるのです。
最近のコンピュータに搭載されているディスプレイはビット・マップ・ディスプレイと呼ばれるもので、下の写真のように「画素」が縦横に綺麗にびっしりと並んでいます。

そのビット・マップ・ディスプレイに文字を表示するのですが、その時「フォント」を使います。文字コードに対応する「形状」を定義したものです。フォントを用いて文字コードを表示用の「形状」へ変換し、それをビット・マップ・ディスプレイの各画素へ書き込むことで、人が目で見て文字であると認識できるようにしているのです。
最も単純なフォントはビット・マップ・フォント(*2)です。画素の並びで文字の形状を表現します。
例えば、下記はビット・マップ・フォントの一部です。
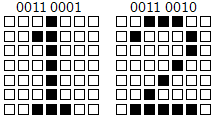
ASCIIコードの0011 0001を画面に表示する場合、このコードに対応する上記の 1 の形状をビット・マップ・ディスプレイへ書き込むことで表示するのです。
なお、そのための命令の内、C++の標準規格で決められているのは「標準出力std::cout」や「標準エラー出力std::cerr」への出力だけです。ここに出力された文字は、コマンド・プロンプトや端末を制御しているプログラムがそれぞれのウィンドウへ描画します。
通常のウィンドウへ出力する場合は、OSやウィンドウ・システム毎に異なるAPIを使う必要が有ります。
(*2)フォントの種類
ビット・マップ・フォント以外に、TrueTypeフォントやOpenTypeフォント等様々なフォントがあります。それぞれメリット/デメリットがあり、場面に合わせて使い分けられています。一般にビット・マップ・フォントは軽いのですが、拡大や縮小すると汚くなります。その問題を解決したフォントがTrueTypeやOpenType等のフォントです。文字サイズを変えても綺麗に表示できます。
現代のコンピュータのほとんどは数値を2進数で記録します。3進数やアナログで記録するコンピュータはほとんどありません。(皆無というわけではないようですが、お目にかかることが出来る人はあまりいないと思います。)
しかし、2進数で表現する場合でも、実は幾つかの表現方法があります。
正の数は皆さんもご存知のように、0から1ずつ増やした時に0000, 0001, 0010, 0011, 0100,…のように増えていく2進数で記録します。そして、負の数は2の補数表現を用いるコンピュータが大勢を占めます。
しかし、定数を加えて負の数を正の値で表現し(ゲタ履き表現)たり、負の数には1の補数を使ったり、絶対値で表現して符号を別途記録したりする方式なども考えられます。C++はそれらのコンピュータを排除しないため、標準規格で決められた制約を満たす限り内部表現は自由です。
特に浮動小数点数はフォーマットを決める際に決定しなければならない項目が多く、様々な方式が実際に存在しています。
しかし、現在ではIEEE 754のフォーマットが事実上の標準となっています。C++でも多くの処理系がIEEE 754を採用していると聞きます。
このように具体的な内部表現方式は処理系依存です。ですので、プログラムを開発する際、可能な場合には内部表現に依存しないようにしておくと、多くのコンピュータで動作するプログラムになるので好ましいです。
今回は下記を解説しました。
- コンピュータは2進数で数値を記録するものがほとんどである
また、一口に2進数と言っても実際の数値表現方法は様々であり、どの方法を用いるのか処理系に任せられている。 - それを人が理解しやすい10進数の文字列に変換して、人とやり取りする。
この10進数や他の進数との変換は標準ライブラリが自動的に行っている。
そして、10進数や16進数等はあくまでも「文字列」としての表現です。各種の変数や計算結果の値は数値であり、それは 1.の仕組みで記録されます。
「10進数変換 アルゴリズム」等で検索すると、「10進数→2進数変換」等の解説サイトが多数出てきます。
多くは、10進数=数値、2進数=文字列の意味で使っています。しかし、コンピュータの内部表現された数値は決して10進数でありません。数値を表示する時に自動的に10進数へ変換されるため、まるで10進数で記録されているかのように見えますが、そんなことはありません。惑わされないようにご用心下さい。
さて、今回、文字コードのもう少し深い部分まで進めようと思っていたのですが、やはり懸念した通り量が多くなりすぎましたので文字コードについては次回解説します。
特に漢字等のワイド文字では様々な頭の痛い問題があります。知らないとハマりやすいものが多いので、この機会に解説したいと思います。お楽しみに。

